New-CVT Theory

Theory

Mathematics in movement, an impossible dance comes true

Jump directly to:
   Ratio range and Number of unique ratios
   The conical involute gear type
   The multi-ratio gear type
   The new CVT
   Conical involute gears, and their relation to 2D gear terminology
   Why previous patents failed

For those seeking a good traditional explanation on current involute gear technology:
tec-science.com
khkgears.net

Ratio range and Number of unique ratios

The new-CVT has a big ratio range with lots of in-between ratios.

The ratio range is easy to calculate, but for your convenience the table below lists the most common ones. Horizontally select the number of teeth of the first gear, vertically select and the number of gears. So for example: a main gear starting with 6 teeth and with 13 gears has a ratio range of 1:1 to 1:25.

Ratio range: Number of teeth of the first gear / Number of gears

6 8 10 12 14 16 18 20 22 24 26 28 30

1 1 1 1 1 1 1 1 1 1 1 1 1 1

2 1.78 1.56 1.44 1.36 1.31 1.27 1.23 1.21 1.19 1.17 1.16 1.15 1.14

3 2.78 2.25 1.96 1.78 1.65 1.56 1.49 1.44 1.4 1.36 1.33 1.31 1.28

4 4 3.06 2.56 2.25 2.04 1.89 1.78 1.69 1.62 1.56 1.51 1.47 1.44

5 5.44 4 3.24 2.78 2.47 2.25 2.09 1.96 1.86 1.78 1.71 1.65 1.6

6 7.11 5.06 4 3.36 2.94 2.64 2.42 2.25 2.12 2.01 1.92 1.84 1.78

7 9 6.25 4.84 4 3.45 3.06 2.78 2.56 2.39 2.25 2.14 2.04 1.96

8 11.11 7.56 5.76 4.69 4 3.52 3.16 2.89 2.68 2.51 2.37 2.25 2.15

9 13.44 9 6.76 5.44 4.6 4 3.57 5.06 2.98 2.78 2.61 2.47 2.35

10 16 10.56 7.84 6.24 5.22 4.52 4 3.61 3.31 3.06 2.86 2.7 2.56

11 18.78 12.25 9 7.11 5.90 5.06 4.46 4 3.64 3.36 3.13 2.94 2.78

12 21.78 14.06 10.24 8.03 6.61 5.64 4.94 4.41 4 3.67 3.41 3.19 3

13 25 16 11.56 9 7.37 6.25 5.44 4.84 4.37 4 3.7 3.45 3.24

The number of possible pinion positions is simply the square of the number of gears. However, quite a few result in the same gear ratio. These are useful to make gear changes quicker, but to get the number of unique gear ratios we use the table below. For example: a main gear starting with 6 teeth and with 13 gears has 115 unique gear ratios.

Unique gear ratios: Number of teeth of the first gear / Number of gears

6 8 10 12 14 16 18 20 22 24 26 28 30

1 1 1 1 1 1 1 1 1 1 1 1 1 1

2 3 3 3 3 3 3 3 3 3 3 3 3 3

3 7 7 7 7 7 7 7 7 7 7 7 7 7

4 13 13 13 13 13 13 13 13 13 13 13 13 13

5 21 21 21 21 21 21 21 21 21 21 21 21 21

6 27 29 31 31 31 31 31 31 31 31 31 31 31

7 37 37 43 39 43 43 43 43 43 43 43 43 43

8 45 51 51 53 57 53 55 57 57 57 57 57 57

9 61 59 67 65 69 67 71 71 73 69 73 73 73

10 69 77 79 77 83 85 85 89 89 83 91 91 87

11 89 89 93 91 103 97 105 105 105 93 111 103 105

12 101 101 107 113 115 119 119 123 127 125 125 123 127

13 115 117 131 127 139 133 137 143 151 141 147 147 147

The gear ratios are not evenly spread, but in a log-normal distribution around the centre. This is convenient as the required speed outputs are also log-normal distributed, by which we mean that they are only seldomly at the extremes. Cars for example hardly ever go at 1 km/hour or at 200 km/hour.

The conical involute gear type

basic shape of all involute gears

The conical involute gear type, also know as the beveloid or tapered gear, is very simple. But it can seem very difficult to understand if you approach it in the wrong way.

For example, mathematically the conical involute gear type can be described as: a 3D involute gear, wherein all the involute curves are aligned in the two dimensional plane, wherein each point in these involute curves extends into the third dimension in a straight line of which the two dimensional component is perpendicular to the involute curve and of which the third dimensional component is tilted at a constant (meaning the same for all the involute points in the 3D gear) angle to the two dimensional plane whereby this constant angle of the third dimensional component is neither perpendicular (would result in a spur gear) nor parallel to the two dimensional plane.

If you were to use this description as a starting point for understanding the conical involute gear type, then you would never really understand it. It is very elegant and clever, but it also hides the very simple basic structure that lies beneath it. Also ignore the literature (it has quite a few pitfalls) for a moment and follow our logic instead.

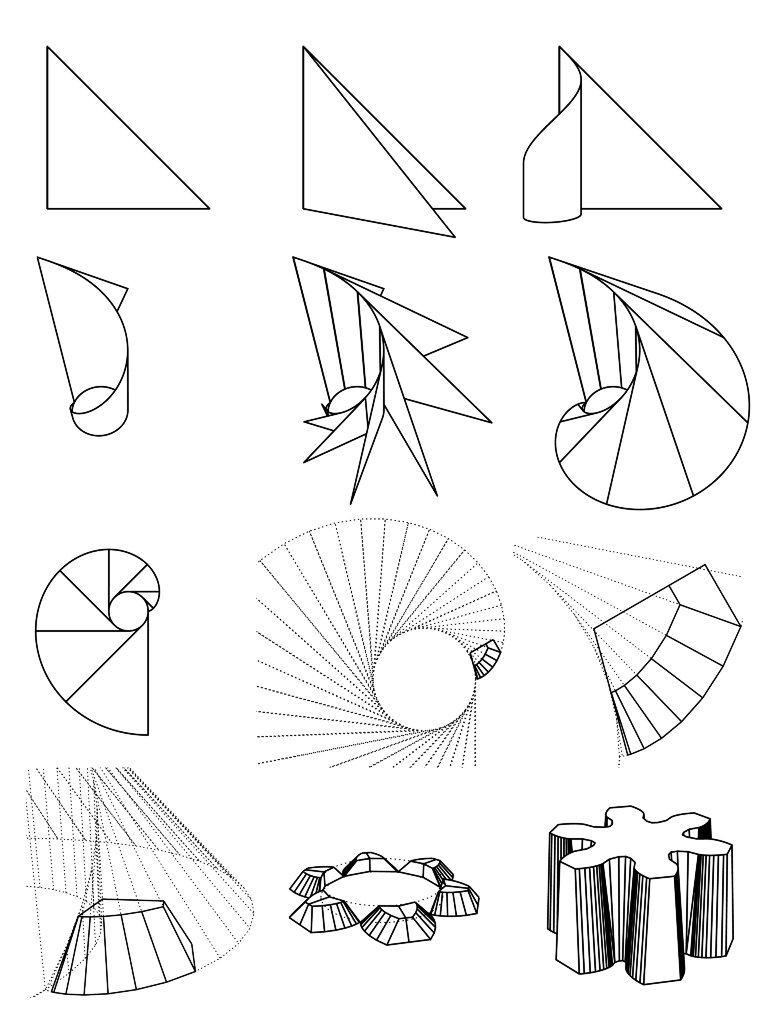
High resolution version (12000 x 16000)

Let's start with a triangle (top left picture), with a horizontal and a vertical line of the same length and with both of them at right angles to each other. It is however the diagonal line that really matters. For it is this line that will be transformed into our final shape after copying, cutting, pasting and rolling. So watch this diagonal line in all its transformations!

In the second picture we have pealed the triangle open to create a second triangle of the same size and shape as the first one.

In the third and fourth picture we have rolled this second triangle into a cylinder.

In the fifth picture we have placed a lot of triangles at the side of the cylinder. They only differ with the first triangle in that their size is such that their heights match that of the cylinder at that position.

The sixth picture is like the fifth picture, except that the number of triangles is now infinite. The result is the basic 3D involute shape that underpins all involute gears (see the animation at the top of this page), both 2D and 3D. Basically the 3D involute shape is nothing more than a straight line spiralling up. By stretching, cutting and mirroring, any basic involute tooth shape can be made from this shape.

The seventh picture is a top view of the sixth.

The eighth, ninth and tenth picture all show the same situation from different viewpoints and what we see is our 3D involute shape from the seventh picture with a lot of it cut away. The removed parts are shown as dotted lines. The top has been sliced off, there is a vertical cut from the centre of the cylinder and if you look very closely, though this cut is not really important, there is also a cut down the line from the top where the 2D involute curve starts. The resulting remaining shape is what will become the contact surface of one tooth half. It is important to realise that all the basic characterises of the 3D involute shape remain intact, even in this small fraction of it.

In the eleventh picture we have mirrored the remaining part from the tenth picture, and then copied it six times while going round. We now have the basic mathematical shape of a conical involute gear with six teeth.

For the twelfth picture we have jumped directly to the finished product. Quite a bit has happened to it, but nothing that would surprise anyone familiar with gear production. Our basic mathematical shape has been stretched considerably in the vertical, the tips cut off (as well as a bit from the top) and metal was added to the centre to connect all the teeth and make it strong. Note that we cut off the tips at the same angle as the intermeshing line (the diagonal from picture one) at that position. This does not always need to be the case, as you will see later.

At this point we have covered the basics of the conical involute gear. But there are few more important aspects to it if you which to create and intermesh them (see the source code for an example).

Intermeshing involute gears can be visualised as two rotating cylinders with a crosswise line between them going up at a constant speed. In both conical and spur gears this line is straight, and in spur gears this line is also vertical.

When drawing conical gears it is practical to relate all the units of distance to the unit of the number of teeth. Basically this means that we base the shape of the conical gears on the 3D involute shape with a base cylinder radius of the number of teeth. This way a gear with one tooth in this unit more will also result in a base circle radius of one tooth in this unit more. And down one tooth in this unit in height will also result in a base circle equivalent of one tooth in this unit more. After the basic shape of the resulting gear has been created, it can be stretched and resized to fit the application.

Intermeshing 3D gears are a beautiful play of mathematics in time and space. It is very simple at hart, but getting to grips with it mathematically can be a bit of a challenge. The trick is to find a point in time and space which is simple, well defined, and that you can base all else on.

If you look at the two pictures below you will see the same situation in two different ways. It shows two identical conical involute gears intermeshing. The circle parts left and right in each picture, show the base cylinders of the gears, while the two diagonal lines are the two planes of action between the two gears. If you look at the animation on the contact page of our website, you will see the intermeshing contact surface (a straight line) between the two gears move along these planes of action at a constant rate. You will also notice that these planes of action are always at right angles with the intermeshing involute curves as seen in 2D.

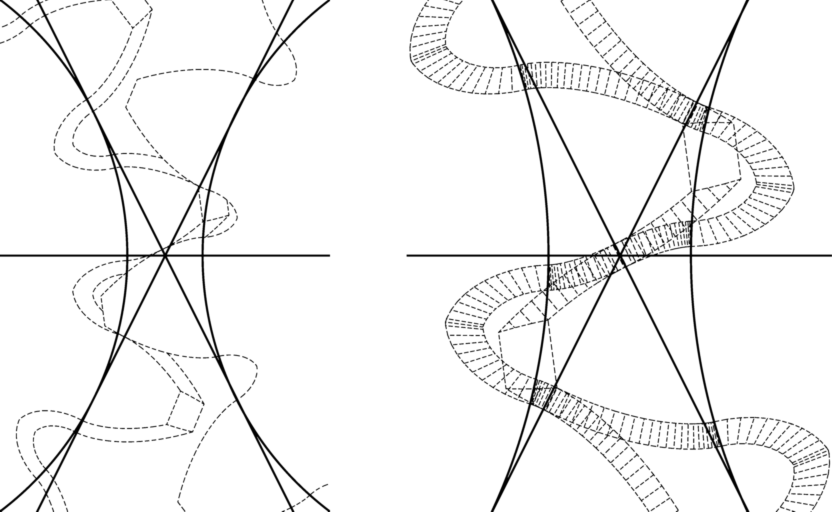
High resolution version (4160 x 2560)

Back at the two pictures above and will notice that there is a lot of symmetry going on. At this point in space and time the whole situation mirrors itself through both the planes of action as well as the horizontal divide. This extreme symmetry exists because at this point in time and space both gears are at exactly the same point in their rotation. It is also the point at which both intermeshing teeth are exactly at the halfway point in their rotation. So all the variables for both gears are the same and we can therefore treat them as being equal and the same. Mathematically this is really useful.

So in a movement where everything is moving in relation to everything else, this is a point where everything is known.

This point is also known as the pitch point and it is traditionally seen as the point at the centre of the crossing lines in the two pictures. Note though that with conical involute gears it is more the point of symmetry in time and space that is show in these pictures, rather than an actual point of intermeshing contact as is the traditional view.

For the traditional interpretation of the pitch point in relation to conical involute gears would result in the surface area line at which the gears are in intermeshing contact with each other, having a changing amount of pressure angle over its length (the so-called operating pressure angles). This would however be incorrect and lead to a lot of problems. So for conical involute gears it is wise to speak of a centre pressure angle at a centre height in conical involute gear. And this centre height and centre pressure angle are the height and pressure angle on the gear at the symmetry point in time and space (the cross point of the three lines in the pictures). We define these two terms solely to avoid misconceptions between the terminology used for 2D spur gears and the terminology used for 3D conical involute gears.

We will leave the rest of the maths to the source code but note that at the symmetry point, and by using the centre pressure angle and the centre height, 2D formulas for spur gears are valid.

This formula calculates the pressure angle of two intermeshing gears from the number of teeth in each gear and the distance between the axes.
Number of teeth in gear A = nA
Number of teeth in gear B = nB
Distance between the axes of the gears A and B = dAB
pressure angle = pa = arccos((nA+nB)/dAB)

This formula calculates the pressure angle from the number of teeth and the reference circle radius.
Number of teeth = n
Reference circle radius = rcr
Pressure angle = pa = arccos(n/rcr)

This formula calculates reference circle radius from the number of teeth and the pressure angle.
Number of teeth = n
Pressure angle = pa
Reference circle radius = rcr = n/cos(pa)

This formula calculates the angle at which the involute curve starts on the base circle at the top of the gear from the number of teeth and the pressure angle at the top of the gear.
Number of teeth = n
Pressure angle at the top = pa
Start angle = sa = (pi/2·n) + tan(pa) - pa

This formula calculates the angle at which the involute curve starts on the base circle at the top of the gear from the radius at the top, the radius in the centre and the centre pressure angle.
Centre pressure angle = pA0
Radius in number of teeth at top = rT
Radius in number of teeth at centre = rC
Pressure angle 1 = pa1 = arccos(cos(pA0)·2·rC/(rC+rT))
Start angle 1 = sa1 = (pi/2·rC) + tan(pa1) - pa1
Start angle 2 = sa2 = (pi/2·rC) + tan(pa0) - pa0
Start angle reference zero = sa0 = 2·sa1 - sa2

We used the above formula for the gears in the new-CVT (height = 3), with:
Number of teeth = n
pA0 = arctan(1/2)
rT = n
rC = 1.5 + n

The multi-ratio gear type

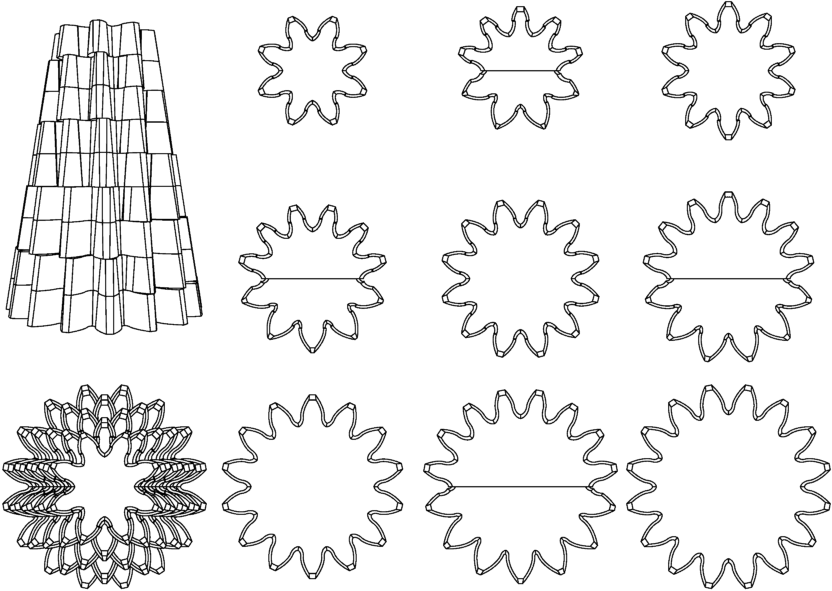
High resolution photo (8320 x 4840)

The animation shows two gears intermeshing perfectly. However, you will have noticed that the blue and green gear on the left is not a normal gear. The green half is from a gear with 10 teeth, while the blue half is from a gear with 12 teeth. The result is that as these two gears rotate, the gear ratio continuously cycles between two different gear ratios. That is why we call the left gear a 'multi-ratio gear' (patent pending).

Lets look at this multi-ratio gear in more detail.

As you can see, the blue and green half of this gear, intermesh perfectly with the gear on the right. For the blue half this is not surprising as it was taken from a normal gear that normally intermeshes with the gear on the right at this distance between the axes. But the green half is from a gear with 10 teeth, and such a gear normally needs a shorter distance to intermesh correctly with the gear on the right.

However, the distance between the axes was increased by profile shifting. Basically this means that the two sides of each tooth on the green gear half were rotated a bit further away from each other. So the teeth became bigger and the holes between the teeth became smaller. The dark green gear half shows the normal outline without profile shifting.

The moment of changeover between the two gear halves is important (pause the animation and scroll back to the first picture). At this moment the red gear simultaneously intermeshes perfectly with both the blue and green half of the gear. For this to be possible three things are important. 1. Both donor gears need to have an even number of teeth. 2. The donor gears need to be cut precisely between two adjacent teeth to the centre of the gear (creating two identical halves). 3. The pressure angles with which the gears were created, and the distance between the centres of the right and left gear needs to be just right. The formula for calculating these is:

Number of teeth main gear = rA
Number of teeth pinion gear = rX
Intermeshing distance = d = sqrt((((2·rA+2)²·((rA+2)²-rA²))/(rA+2)²)+(rA+rX)²)
Pressure angle pa = arccos((rA+rX+2)/d)

See the source code for more info.

Lastly there is one more point. The holes between the teeth are called roots. And the roots at the border between the blue and green half are the ones from the blue half. In fact we didn't quite cut trough the middle, but a little higher so we included the root from the blue half. The reason being that, just before the gear on the right starts to intermesh with the green gear, there is a short period in the cycle where the gear on the right would cut into the green gear half, as the speed of the left gear is at that moment still determined by the blue half. So the root cut of the first (and last) tooth of the green gear needs to be a bit bigger. And in the 2D version of the multi-ratio gear, the normal root cut for the blue half is just big enough (the 3D version needs a slightly bigger root cut). So in this case it is possible to make the actual cut trough the halves a little more inside the green half as it makes the left gear easier to produce. Conceptually though they are two halves, with the first and last root cut of the gear half with less teeth being a bit bigger.

If you look very closely at the switch-over point between the two halves you will notice a little backlash that was created by making the roots bigger at this point. Theoretically, in 2D, there is no backlash in the rest of rotational cycle.

The new-CVT

High resolution version (16000 x 12000)

Here we see the idea of the multi-ratio gear and that of the conical involute gear combined into the new type of transmission that we call the 'new-CVT'. We see a cascading set of gears whereby each next gear has one more tooth than the previous. The gears with an even number of teeth are normal conical gears, while the ones with an odd number of teeth are multi-ratio conical gears.

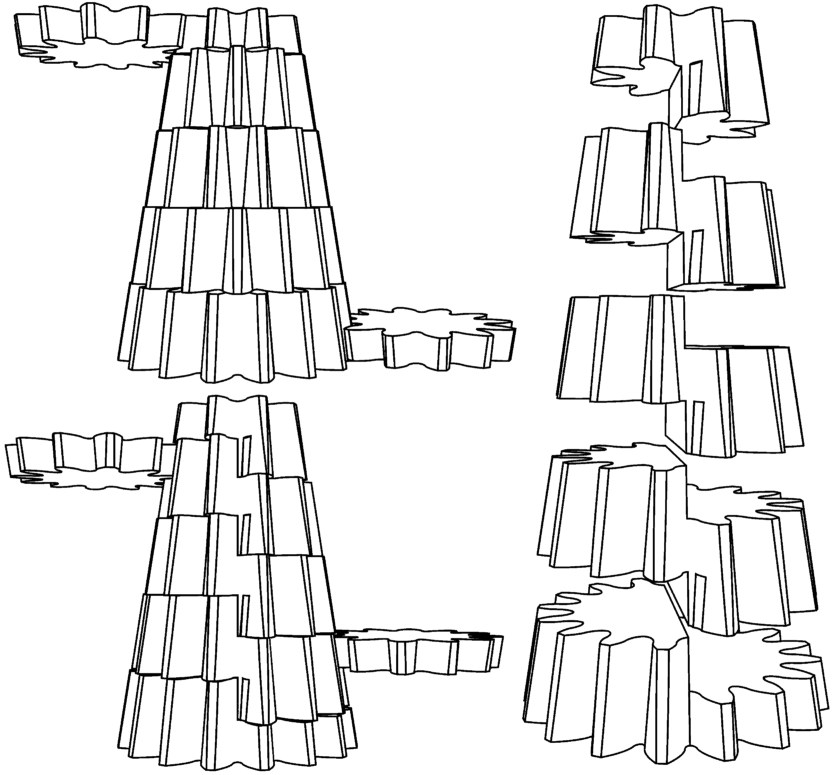
High resolution version (5921 x 5514)

However, if we look at the above figures, we notice that all the gears are in fact gears with an even number of teeth. It is just that by cutting off a bit of the top and bottom half of these gears, and extending the remaining half into the vertical range of the neighbouring gear, that the multi-ratio gears with an odd number of teeth were created. We also notice the slightly bigger roots at the bottom half at the switch-over border to prevent inter cutting.

The two pinion gears at the sides of the main gear have rotational axes that are parallel to that of the main gear, but they can also slide vertically over the main gear via a straight line that is at a slight angle to the rotational axes. This allows them to use the multi-ratio gears as intermediate stages between the normal gears. So by sliding at the right times (see the animation on the home page), they can slide vertically to any position on the main gear. And as there are two pinions, one to drive the main gear and one to take drive from it, there are very many possible positional combinations. This is what creates the great number of different gear ratios of the new-CVT.

There are a few aspects to this system that are not directly obvious from the figures.

The donor gears comprising the main gear are all calculated for a height of three teeth (the top part of the top gear and the bottom part of the bottom gear are deleted after the calculation). While the difference in teeth between the cascading parts is two teeth. And as the gears are height-wise divided in three, this means that a pinion with a maximum height of one tooth can intermesh perfectly with any of the three parts separately. 0 to 1 tooth for the top part, 1 to 2 for the middle part and 2 to 3 for the bottom part. So the height difference in a 2D cut out between the cascading gears is always exactly two teeth (for example: 2.5 switching to 0.5).

The centre pressure angle of the gears in the main gear is arctan(1/2). Other centre pressure angles are possible, but it was found that this was the optimum angle that led to the least backlash. We also used arctan(1/2) for the pinions in our demo but this is not a requirement.

The tips of all the gears (main gear and pinions) are cut at the same angle as the angle of the line over which the pinions slide vertically.

The half cut at the top and bottom of the gears in the main gear can be at a different rotational position. For example, placing both halves above each other could enable quicker gear changes.

The root cuts at the switchover points are a little more enlarged than in the 2D multi-ratio gear because the 3D version is not theoretically perfect, but this is no problem as the backlash is still very small (see the animations). The very small extra cuts next to the enlarged root cuts are artefacts of how the gears were created, they are have no function.

Conical involute gears, and their relation to 2D gear terminology

Conical involute gears can be seen as the basis of all involute gears. Spur gears for example are only a special case of conical involute gears (the tilt angle is perpendicular to the two dimensional plane). However, a lot of gear terminology dates back from before conical involute gears were invented and it can therefore seem confusing in the light of conical involute gears.

For example when examining a range of two-dimensional cut-troughs of a conical involute gear taken at different heights, one can see that both the pressure angle and the profile shifting amounts change with the vertical position of the cut-trough. So obviously 'pressure angle' and 'profile shifting' are related, but in 2D terminology these are two very different things! Add to that that each conical involute gear simultaneously intermeshes at a whole range of different pressure angles and at a whole range of different profile shifting amounts, and it becomes clear that 2D gear terminology can be highly confusing when it comes to conical involute gears.

However, this does not mean that 2D gear terminology is useless when it comes to conical involute gears. For example, the 2D gear formula for calculating the distance between intermeshing gears is very useful. But it does require some extra care in order for it to be useful in regards to conical involute gears.

The 2D profile of conical involute gears changes over their vertical axes. Furthermore the gears that they intermesh with are upside down as compared to themselves. So the pressure angles and profile shifting values change in opposite directions between intermeshing gears. Therefore, there is at the most only one vertical position where the pressure angles are the same. To make things easier it is a good idea to define the pressure angle at the centre height of a conical involute gear as the 'centre pressure angle' of the gear. So if two gears intermesh with their centres facing each other, and both gears have the same (default) centre pressure angle, then 2D involute theory can be used at that 2D cut trough height. However, you will have realised at this point that conical involute gears can slide over each other vertically, so what happens if they do so? That is a good question and one that is not so easy to answer... 2D gearing traditionally assumes that the same (default) pressure angle applies everywhere, but with conical involute gears this assumption only holds true for one special case.

It is important to realise that 2D gear terminology and technology has come from practical application, while conical involute gears as we introduce them here are based on the mathematical 3D involute shape. So they are very different. What is fundamental to the one, will often seem but a mere side effect to the other. For example, within conical involute gear theory, the base circle is of the up most importance while the pressure angle and the reference circle are almost ignored (not to mention the modulus). Take a look at the source code to get an idea of how different the new approach is.

As you might have guessed by now, we also invented the 3D tilted gear. But later found that this already existed and that it is called the conical involute gear. This is the main reason why our approach is so different, we started from a blank sheet.

Why previous patents failed

US3608390 Arthur G Barrett 1971

Theoretically "US3608390A" is incorrect and it only somewhat works in practice due to design choices (many teeth and a lot of backlash) that make it practically useless (very small gear ratio range, vibration in the output). My application could not be built based on in the information contained in "US3608390A". Therefore I see "US3608390A" more as a description of desired function, rather than as an explanation of how to actually achieve this desired function.

Main problems:

Conical involute gears can only correctly intermesh if:

both gears are conical involute gears
the conical involute gears point in opposite directions
the axes are parallel (the planes of action of both gears need to overlap and this condition is only true if the axes are parallel).

"US3608390A" fails on all three points.

Also it does not have the enlarged roots at the borders between the gear halves of those gears that try to function as multi-ratio gears.

US9027427B2 Panayiotis Economou 2015

Here you see why conical involute gears are essential. This has many problems.

Video

Very nice animation that cannot work